Part 5 Performance Metrics (accuracy, precision, recall F1 and ROC), and Logistic Regression
- Rodrigo Ledesma
- May 15, 2022
- 9 min read
Updated: May 19, 2022
Link to the google colab: https://colab.research.google.com/drive/1YYeNlJaouUkxBT4ELeT0aPLVsFa97nVJ?usp=sharing
Welcome back to another post on the series on predicting waiting times in amusement parks. Today we are ready to train our first model, We will be using a simple algorithm called Logistic Regression. There are many different types of regressors, among the most popular, are logistic linear and polynomial. In this post, we will be using a Logistic, because we need to predict non-continuous values, or in other words, we need to perform classification. So our model will choose from a group of pre-established values.

You guessed correct, we will be choosing time intervals from our Harry Potter Ride dataset. If we do a little research in the feature, we will see that the web page offers waiting times in 5 minutes intervals. And also the waiting times are always integer numbers multiples of 5. Using python’s .unique() function we can see that we have the following categories:
5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 105 110 115 120 145 150 180
Logistic Regression
import pandas as pd
from sklearn.model_selection import train_test_splithp_ohe = pd.read_csv("harryPotterCleanOHE.csv")
hp_oe = pd.read_csv("harryPotterCleanOE.csv")
hp_me = pd.read_csv("harryPotterClean.csv")def getXandY(df):
df.drop(df.tail(20).index,inplace=True)
x = df.drop(['Harry_Potter_and_the_Forbidden','Unnamed: 0'],axis=1)
y = df.Harry_Potter_and_the_Forbidden
return(x,y)def trainTest(x,y):
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.30, shuffle=True)
return(X_train, X_test, y_train, y_test)As you can see, the code is pretty simple and I just got the 3 data frames with different encodings, then I created 2 functions, one for splitting X and Y variables and another to make the train and test df. Let’s see what is going on in the first function but it is pretty straightforward. First, we get rid of the null values, then we drop the target variable and the index variable to create our X dataset or our independent variables. Then we just grab the target feature and put it into the Y dataset.
For the train and test, sklearn makes our lives easier by providing a function to perform this action. So we import the function and we create 4 different dataframes, two for training and 2 for testing, the important part here is that in test_size, we configure how big this set should be. In this case, I chose the testing to have 30% of the complete raw dataframe. And one very important part is the shuffle, this command will allow us to have different values in every created dataframe every time we run the function. This will be super useful to create different models, based on different parts of our data.
Easy like winning a match against the Senators!
x,y=getXandY(hp_me)
X_train, X_test, y_train, y_test = trainTest(x,y)from sklearn.linear_model import LogisticRegression
from sklearn import metricslogisticRegr = LogisticRegression(max_iter=20000)
logisticRegr.fit(X_train, y_train)
y_pred=logisticRegr.predict(X_test)We make use of the functions previously described and we import the logistic regression library from sklearn. Its implementation is very straightforward, we need to create an LR object and in this case, my script was failing because the number of iterations was being maxed out. So I just defined a huge number of max iterations (bigger than my actual dataset). I fit my model and finally, I store the predictions for testing in y_pred.
So far, we have a trained model, and also we have its predictions, so based on them we need to evaluate our model, for this, we will use 4 different parameters. Confusion Matrix, Accuracy, Recall, and Precision.
Confusion Matrix:
This is a visual evaluation method. It consists of a table with dimensions n x n where n is the number of features. The table in general divides into 4 main sections. The first section is the True Positives, it will count the number of times the model predicted a positive outcome and the true value was also positive. For example for our model, this value will be the number of times the model predicted 5 minutes, and it actually was 5 minutes. True Negatives; this parameter will count the number of times the model predicted a false and the result was actually false. For understanding this concept a binary classification is actually better. For example, if we are trying to predict if a patient has cancer, a true negative will be when the model predicted they do not have it, and actually, the patient was cancer-free. Then we have the incorrect section of the matrix, where we will be storing the False Positives and the False Negatives. A FP is when the model predicted a positive outcome but in reality, it was false. And finally, FN is when the model predicted a negative but it actually was positive. These values are very important and depending on the application we might not look to increase the true positives, maybe we will be focussing on decreasing the number of false positives. E.g. when we are making a model that predicts if a tumor is malign it is more important to decrease the number of times we say “you are ok, don’t worry you don’t have cancer” and 3 months later, discover the model was wrong.

Harry Potter Confusion Matrix from Logistic Regression
Coming back to our project, the image above shows the confusion matrix result of running our model. If you have some experience you can appreciate the results are not very pleasing. We have approx 700 values predicted as to have a 10 min wait, that were actually only 10 minutes. The rest of the results are very bad. For instance, the model is not able to predict waiting times above 120 minutes. Let’s try out testing the rest of the metrics.
Accuracy
This metric is pretty simple to understand, accuracy is defined as the fraction of predictions our model got correct, the full equation is the following:
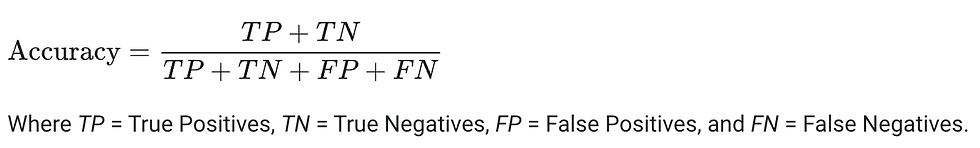
By its own, accuracy can give a good idea of the general performance of our model, nevertheless it does not show the complete picture. We will explain later on what an imbalance dataset is, but for now let’s just say that as our dataset is imbalanced, accuracy doesn’t have the last word. A quick example will be if we have a dataset to classify dogs and cats, but out of 1000 images 900 are dogs, the model will learn that almost everything is a dog. Imagine that you then have created a model that predicts that everything is a dog, missclasifying all the cats. The accuracy of the model will be around 90% but it is a terrible classifier because it fails to actually classify cats. This is what is actually happening in our case with times bigger than 120 mins. Lets see how we can calculate it for our model and also what is the accuracy of the current regression model.
from sklearn import metricsprint("Accuracy:",metrics.accuracy_score(y_test, y_pred))Accuracy: 0.2449195596951736Pretty easy isn’t it? Yes! I know what you are thinking, easy such as winning a match against the Senators! So the accuracy of our model is 25%. Pretty bad, lets see other metrics.
Precision
This metric is defines the relation between the true positives and the sum of all positives. In simple words, the precision indicates which proportion of positive identifications was actually correct. And in human words we can say that precision will help us understand how well the model has classified the feature in question focussing on their positive outcomes. The formula es the following one:

If we are asked to optimize this specific metric will be to minimize the mistakes when predicting positive labels. Let’s take a look at how we can calculate the precision for our model:
print("Precision:",metrics.precision_score(y_test, y_pred,average='weighted'))Precision: 0.15101987536544959Please notice that we have a last parameter in the function, average. We can use different average parameters but as we are attempting a multiclass classification, the weighted average does the work. If you try to do a binary classification you can leave the default value. 15% of the positive predictions were identified correctly, one more time this indicates that our model is not doing the best job.
Recall
To understand recall it is easier to think of a binary classification. Let’s imagine that our purpose is to classify apples and oranges, so the recall will analyze once the classification is done, how many apples were correctly classified, but instead of focusing on the total classification (TP &FP only one side) it will focus in the whole set of apples, it does not matter where they are. Recall gives an answer to the question “What proportion of actual positives was identified correctly?” In this case the metric evaluates the number of positive predictions the model guessed correctly, divided by this same variable and the number or positives the model got wrong. Again in human words we can define recall as how completely the model has found the model in question. Given this let’s see the formula for the recall:

Now how are we going to calculate it with python? Easy!
print("Recall:",metrics.recall_score(y_test, y_pred,average='weighted'))Recall: 0.2449195596951736The result is 25%
Let me make a little parenthesis and explain something about our specific case. The last example we gave regarding apples and oranges was terrific because it can be visual, but for the ride’s time we have more than two classes, do you remember we stated that we are making a weighted average? This means that in this case, we are analyzing each class and making a weighted average.
Now back to our results, the accuracy states that the model predicted correctly 24% of the cases, the precision states that given the positive identifications out of each class 15% were correctly classified, and finally, the recall states that focussing on the actual values of each class (pretending the other classes do not exist) 25% were correctly classified.
F1 Score
In extreme cases if our model predicts everything in a system as positive, then we will have a recall of 100% and a precision of 0%. These metrics are directly correlated, but let’s see one metric we can use to evidenciate easily this relationship and measure both at the same time.
The F1 score is defined as a harmonic mean between precision and recall, and in human words this means how good and complete the predictions are.
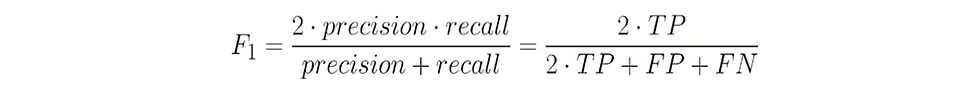
Let’s see what this score says about our model, so lets make the code:
F1= metrics.f1_score(y_test, y_pred, average='weighted')F1: 0.16963133700660507In a minute I will give a complete description of why I am using weighted and not micro or macro, but let’s analyze that the relationship between our recall and precision is poor. All the combinations of our metrics translate in one thing: our model has a poor performance for predicting the waiting times. But before we go into why let’s explain one main concept.
Receiver Operating Characteristic (ROC)
The ROC curve plots the relationship between the true positive rate on the Y axis and the false positive rate in the X axis. The more area under the curve on this plot, the better our model is on predicting values correctly.
As we are making a multiclass classification, implementing this metric in python is not as straight forward so let’s start by the very beginning as my aunt Julie Andrews used to say (if you did not understand maybe you are too young don’t worry).
The first step will be to binarize our y_test dataset, and by this I mean that we will be creating an array where each element will represent a binary category (0 in the first space will represent this value is not 5 min, 1 in the second space will represent this value is a 10 min and so on). This will be achieved with the following lines:
from sklearn.preprocessing import label_binarizey_test_bin = label_binarize(y_test, classes=[5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110,115, 120, 135, 150, 180])These lines will produce the following output:

As you can see we have an array of arrays where each element in the array represent a class. And the place where the value is true, represents the actual class.
logisticRegr.fit(X_train, y_train).decision_function(X_test)
y_pred_proba = logisticRegr.predict_proba(X_test)
y_pred_proba2= np.delete(y_pred_proba, numpy.s_[27:], axis=1)Next, step is very important, the y_pred variable, has only the result of the most likely class, and in this case we don't need that. What the ROC function needs is an array with all the classes’ probabilities (which must sum to 1) And todo this, we use the .predict_proba() function. Then I delete some values that were unnecessary for my analysis and then proceed to make the ROC analysis.
To calculate the ROC value we need to remember we are working with multiclassification and therefore it is necessary to give the function all the necessary information. In order to make the function run correctly, let’s add the element “multi_class” which can be one versus one(ovo) or one versus rest (over). Fortunately for this specific case, it doesn’t matter which one we pick because the results are the same but let’s see how well out model performed on the relationship between TPR and FPR:
# Compute ROC area for each classmacro_roc_auc_ovo = roc_auc_score(y_test_bin, y_pred_proba2, multi_class="ovo",average='weighted')
macro_roc_auc_ovr = roc_auc_score(y_test_bin, y_pred_proba2, multi_class="ovr",average='weighted')macro_roc_auc_ovo
0.590597313963011macro_roc_auc_ovr
0.590597313963011As we can appreciate, the ratio (the area under the curve is almost 60%. Not the best, definitely we can improve it. This value is definitely enough for our analysis but just for fun let’s plot the ROC curve.
# Compute ROC curve
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y_test_bin[:, i], y_pred_proba2[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])# Compute weighted-average ROC curve and ROC area
fpr["weighted"], tpr["weighted"], _ = roc_curve(y_test_bin.ravel(), y_pred_proba2.ravel())
roc_auc["weighted"] = auc(fpr["weighted"], tpr["weighted"])plt.figure()
lw = 1
plt.plot(
fpr[2],
tpr[2],
color="darkorange",
lw=lw,
label="ROC curve"
)
plt.plot([0, 1], [0, 1], color="navy", lw=lw, linestyle="--")
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("Receiver operating characteristic example")
plt.legend(loc="lower right")
plt.show()
This is the end of this post, on the next one we will be analyzing the average possibilities and also that an unbalanced dataset is.



Comments