Part 7 Principal Component Analysis
- Rodrigo Ledesma
- May 15, 2022
- 9 min read
Updated: May 20, 2022
Hello! Welcome to this new section of my blog, and thank you if you have been reading my post so far. Today we will be continuing with Part 4, where our purpose was to filter and select only the most relevant variables to train our model.
If this is the first time you visit my blog, the purpose of this series of articles is intended to create a Machine Learning model to predict how long will it take an average visitor to wait in line at a Disney or Universal park before they can ride their favorite rollercoaster and with this information, optimize their visit by scheduling parks in the day where their favorite parks are less crowded. Before we analyze which feature selection technique is the best for our dataset, please introduce one popular technique, but a little more complicated.
Principal Component Analysis PCA
By now, there should be thousands of blogs explaining how to use PCA and what it is, but most of them use the iris dataset or MNIST and we will be handling the rough part, using it in a different dataset. Thanks to sklearn the actual implementation of the technique can be summarized in a couple of lines, but the important part is to understand what it does and how so that we can comprehend if it complements our analysis.
My favorite article describing the technique was written by Zakaria Jaadi last year, feel free to visit his article, as he makes a hell of a job with the description. Not too mathematical and not too shallow.
https://builtin.com/data-science/step-step-explanation-principal-component-analysis PCA description
The principal component analysis is a technique to reduce the dimensions of a set of data, we can use it to trim the number of features in a dataset to make the training process quicker, or to visualize a set of data into a 2 or 3 dimension graph, even to create inorganic features to represent data.
This is extremely important, please, the first thing you need to do is to standardize your data, as the PCA method will behave differently if you don’t. Once the dataset is standardized, now we will begin. PCA is a statistical method based on the amount of variance and the amount of information a variable contains. Variance is also a statistical method to calculate how to disperse a set of values is with respect to their mean, the variance is closely linked to the standard deviation as they are only separated by a square root.
The more dispersed a dataset is, the more information it contains, but PCA does not calculate only the variance, as this is a measurement of the same variable, what PCA actually calculates is the covariance, which defines the amount of dispersion a variable has with respect to another. This is actually more useful, as the result of covariance will tell us if there exists a relationship between the two variables.
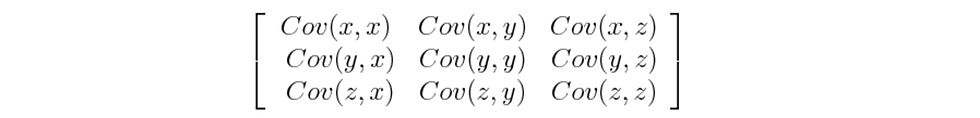
PCA will calculate a matrix of covariances where each cell will contain the result of all combinations of covariances. Something important to state is that if the covariance is a positive number, then the two variables are correlated, they increase or decrease together, now in the other hand, if the result is negative, they are inversely correlated if one increases the other one decreases. PCA focus on those variables which have big variance and to better explain why I will site my favorite ML book “Hands-on Machine Learning with Scikit-learn and TensorFlow” by Geron Aurelien. I really recommend that if you have a little experience or even if you are begging you should read this book it is easy, it has a lot of examples, and it covers a great range of topics that are essential. Geron in page 223 has a great image of a 2D projection of data.

Here you can see the 2D representation of data together with different lines that represent the components PCA calculates. You can also see the 3 graphs from Z1, they have different amounts of variance and PCA will choose first the top one, as it has the biggest amount of dispersion and because of this the biggest amount of information.
In this example, there are only 2 dimensions, so there will be only two components, one important thing to mention is that the second component will be perpendicular to the first one, so if we have n variables, there will be n components, each one perpendicular to the last one.
But coming back to our matrix, based on the covariance matrix PCA will then calculate the eigenvalue and the eigenvector. These two new elements always go together, and there will be a pair for each variable analyzed. The eigenvector will be the principal component or the equivalent of the projection in the figure above. Each call in the covariance matrix will have an eigenvector associated, and also an eigenvalue. The eigenvalue will contain a number that represents the percentage of variance or information that each principal component has. Based on these values, we can then choose only those principal components which have for example the 90% of the total information and omit those ones which are not relevant enough. Using PCA for dimensionality reduction with Sklearn.
Let’s get our hands dirty, first let’s do some quick data cleansing, just like the one we did in part 6
Delete outliers
Merge classes ending in 5
Compact classes to have only 6 classes
Apply SMOT oversampling
For this, here is the code, but you know that at the end of the article you will find a link to my colab
import numpy as np
import pandas as pd
from collections import Counter
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from imblearn.over_sampling import RandomOverSampler, SMOTEhp_me = pd.read_csv("harryPotterClean.csv")#Function to perform oversampling
def overSampling(X_train, y_train, y_test, method):
X_train_os, y_train_os= method.fit_resample(X_train, y_train)
# Check the number of records after over sampling
print(sorted(Counter(y_train_os).items()))
return(X_train_os, y_train_os)#Fucntion to split into X and Y
def getXandY(df):
df.drop(df.tail(20).index,inplace=True)
x = df.drop(['Harry_Potter_and_the_Forbidden'],axis=1)
y = df.Harry_Potter_and_the_Forbidden
return(x,y)#Function to split in test and train
def trainTest(x,y):
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.30, shuffle=True)
return(X_train, X_test, y_train, y_test)#Delete all rows which contain outliers
hp_clean = hp_me[hp_me.Harry_Potter_and_the_Forbidden != 0] #delete rows with 0 min
hp_clean = hp_clean[hp_clean.Harry_Potter_and_the_Forbidden != 180]
hp_clean = hp_clean[hp_clean.Harry_Potter_and_the_Forbidden != 150]
hp_clean = hp_clean[hp_clean.Harry_Potter_and_the_Forbidden != 145]
hp_clean = hp_clean[hp_clean.Harry_Potter_and_the_Forbidden != 135]
hp_clean = hp_clean[hp_clean.Harry_Potter_and_the_Forbidden != 130]
hp_clean = hp_clean[hp_clean.Harry_Potter_and_the_Forbidden != 11]
hp_fin_clean = hp_clean[hp_clean.Harry_Potter_and_the_Forbidden != 125]#Replace times ending in 5 and also compacting the rest to have only 6 classes
a=hp_fin_clean.Harry_Potter_and_the_Forbidden.replace([5, 15, 25, 35, 45, 55, 65, 75, 85, 95, 105, 115, 120, 110, 150,80, 90, 50,70],
[10,10, 20, 30, 40, 50, 60, 60, 100, 100, 100, 100, 100, 100, 100,100, 100, 60,100])
#Create the final dataframe
df=pd.DataFrame(a)
hp2=hp_fin_clean.drop('Harry_Potter_and_the_Forbidden',axis=1)
hp3=pd.concat([hp2, df], axis=1)
hp4=hp3.drop('Unnamed: 0',axis=1)
hp4.Harry_Potter_and_the_Forbidden.unique()#Split the compact dataframe into X and Y and train and test
x,y=getXandY(hp4)
X_train, X_test, y_train, y_test = trainTest(x,y)smote = SMOTE(random_state=42)
X_train_os, y_train_os=overSampling(X_train, y_train, y_test, smote)Ok enough code. Let’s stop for a second because now we will do something different, which is to use the PCA Method:
from sklearn.decomposition import PCApca = PCA()
X_train_pca = pca.fit_transform(X_train_os)
X_test_pca = pca.transform(X_test)explained_variance = pca.explained_variance_ratio_
explained_varianceHere let me stop one more time, the line explained_variance is extremely important as it will throw a result similar to this:
array([3.978333e-01, 1.33281207e-01, 1.23483593e-01, 8.93438348e-02, 8.467811e-02, 5.30658669e-02, 4.13933533e-02, 2.69784551e-02, 2.47163e-02, 1.40984199e-02, 1.11274067e-02, 2.61142634e-34])
This array is crucial for our analysis. The first value is the variance of the first principal component, this means that only the first PC has almost 40% of the total information in the system, moving on to the second value means that the second PC contains 13% of the total information, and so on. Now we might want to use the PCs that contain for example 95% of the information by omitting those with low variances such as the last one which contains 32 zeros after the decimal point. But first let’s see what happens if we use all the components for training and evaluating the model:
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
from sklearn.metrics import classification_reportlg = LogisticRegression(max_iter=20000)
lg.fit(X_train_pca, y_train_os).decision_function(X_test_pca)
y_pred=lg.predict(X_test_pca)print(classification_report(y_test, y_pred))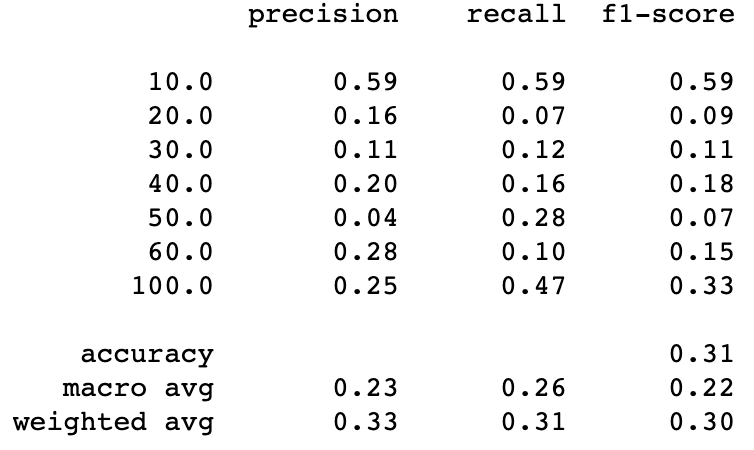
The results are not great, so let’s make a quick function that will do this process but, starting with only the 1st PC, then using the 1st and the 2nd and so on…
def myPCA(n,X_train,X_test,y_train):
print("-------------------------number of components = ", n)
pca = PCA(n_components=n)
X_train_pca = pca.fit_transform(X_train)
X_test_pca = pca.transform(X_test)
lg = LogisticRegression(max_iter=20000)
lg.fit(X_train_pca, y_train).decision_function(X_test_pca)
y_pred=lg.predict(X_test_pca)
print(classification_report(y_test, y_pred))l = list(range(1,13))for i in l:
print(i)
myPCA(i,X_train,X_test,y_train)-------------------------number of components = 1
precision recall f1-score support
10.0 0.33 1.00 0.49 1552
20.0 0.00 0.00 0.00 791
30.0 0.00 0.00 0.00 465
40.0 0.00 0.00 0.00 528
50.0 0.00 0.00 0.00 92
60.0 0.00 0.00 0.00 799
100.0 0.00 0.00 0.00 496
accuracy 0.33 4723
macro avg 0.05 0.14 0.07 4723
weighted avg 0.11 0.33 0.16 4723
-------------------------number of components = 2 precision recall f1-score support
10.0 0.33 1.00 0.49 1552
20.0 0.00 0.00 0.00 791
30.0 0.00 0.00 0.00 465
40.0 0.00 0.00 0.00 528
50.0 0.00 0.00 0.00 92
60.0 0.00 0.00 0.00 799
100.0 0.00 0.00 0.00 496
accuracy 0.33 4723
macro avg 0.05 0.14 0.07 4723
weighted avg 0.11 0.33 0.16 4723
-------------------------number of components = 3
precision recall f1-score support
10.0 0.33 1.00 0.49 1552
20.0 0.00 0.00 0.00 791
30.0 0.00 0.00 0.00 465
40.0 0.00 0.00 0.00 528
50.0 0.00 0.00 0.00 92
60.0 0.00 0.00 0.00 799
100.0 0.00 0.00 0.00 496
accuracy 0.33 4723
macro avg 0.05 0.14 0.07 4723
weighted avg 0.11 0.33 0.16 4723
-------------------------number of components = 4 precision recall f1-score support
10.0 0.34 0.98 0.51 1552
20.0 0.00 0.00 0.00 791
30.0 0.00 0.00 0.00 465
40.0 0.00 0.00 0.00 528
50.0 0.00 0.00 0.00 92
60.0 0.21 0.05 0.08 799
100.0 0.27 0.06 0.09 496
accuracy 0.34 4723
macro avg 0.12 0.16 0.10 4723
weighted avg 0.18 0.34 0.19 4723
-------------------------number of components = 5
precision recall f1-score support
10.0 0.34 0.95 0.50 1552
20.0 0.00 0.00 0.00 791
30.0 0.00 0.00 0.00 465
40.0 0.00 0.00 0.00 528
50.0 0.00 0.00 0.00 92
60.0 0.21 0.06 0.09 799
100.0 0.27 0.09 0.13 496
accuracy 0.33 4723
macro avg 0.12 0.16 0.10 4723
weighted avg 0.18 0.33 0.19 4723
-------------------------number of components = 6 precision recall f1-score support
10.0 0.35 0.93 0.51 1552
20.0 0.24 0.06 0.10 791
30.0 0.00 0.00 0.00 465
40.0 0.00 0.00 0.00 528
50.0 0.00 0.00 0.00 92
60.0 0.19 0.06 0.09 799
100.0 0.28 0.10 0.15 496
accuracy 0.34 4723
macro avg 0.15 0.16 0.12 4723
weighted avg 0.22 0.34 0.21 4723
-------------------------number of components = 7
precision recall f1-score support
10.0 0.37 0.89 0.52 1552
20.0 0.19 0.12 0.15 791
30.0 0.00 0.00 0.00 465
40.0 0.17 0.00 0.00 528
50.0 0.00 0.00 0.00 92
60.0 0.21 0.09 0.13 799
100.0 0.28 0.08 0.13 496
accuracy 0.34 4723
macro avg 0.17 0.17 0.13 4723
weighted avg 0.24 0.34 0.23 4723
-------------------------number of components = 8
precision recall f1-score support
10.0 0.43 0.83 0.56 1552
20.0 0.21 0.10 0.13 791
30.0 0.00 0.00 0.00 465
40.0 0.17 0.01 0.02 528
50.0 0.00 0.00 0.00 92
60.0 0.25 0.35 0.29 799
100.0 0.43 0.17 0.25 496
accuracy 0.37 4723
macro avg 0.21 0.21 0.18 4723
weighted avg 0.28 0.37 0.29 4723
-------------------------number of components = 9 precision recall f1-score support
10.0 0.44 0.82 0.57 1552
20.0 0.20 0.09 0.13 791
30.0 0.00 0.00 0.00 465
40.0 0.19 0.01 0.02 528
50.0 0.00 0.00 0.00 92
60.0 0.25 0.37 0.30 799
100.0 0.37 0.17 0.23 496
accuracy 0.37 4723
macro avg 0.21 0.21 0.18 4723
weighted avg 0.28 0.37 0.29 4723
-------------------------number of components = 10
precision recall f1-score support
10.0 0.44 0.83 0.58 1552
20.0 0.25 0.13 0.18 791
30.0 0.00 0.00 0.00 465
40.0 0.24 0.03 0.05 528
50.0 0.00 0.00 0.00 92
60.0 0.26 0.37 0.30 799
100.0 0.37 0.17 0.24 496
accuracy 0.38 4723
macro avg 0.22 0.22 0.19 4723
weighted avg 0.30 0.38 0.30 4723
-------------------------number of components = 11 precision recall f1-score support
10.0 0.47 0.88 0.61 1552
20.0 0.23 0.12 0.16 791
30.0 0.00 0.00 0.00 465
40.0 0.21 0.05 0.08 528
50.0 0.00 0.00 0.00 92
60.0 0.28 0.35 0.31 799
100.0 0.39 0.21 0.27 496
accuracy 0.39 4723
macro avg 0.22 0.23 0.20 4723
weighted avg 0.30 0.39 0.32 4723
-------------------------number of components = 12 precision recall f1-score support
10.0 0.47 0.88 0.61 1552
20.0 0.23 0.12 0.16 791
30.0 0.00 0.00 0.00 465
40.0 0.21 0.05 0.08 528
50.0 0.00 0.00 0.00 92
60.0 0.28 0.35 0.31 799
100.0 0.39 0.21 0.27 496
accuracy 0.39 4723
macro avg 0.22 0.23 0.20 4723
weighted avg 0.30 0.39 0.32 4723The first thing we need to notice is that the recall of the first 4 calls is 100% for the first class and 0% for the rest, this is because before this value we have not reached 70% of information or variance in the variables ensemble. Afterward, the recall improves. Another point that is important is to notice that using 11 and 12 PC is the same, so there is no point in using the last one. The last observation will be that as we have a balanced dataset, we must focus our attention int the macro avg, which gives the same weight to each class for the analysis. Based on this parameter, the best result is obtained with 11 components, also here we have the best accuracy. So this is the winner, but let’s not sing victory yet, as we have a lot more techniques to analyze.
Link to google colab: https://colab.research.google.com/drive/1H0M0eQX1c1Wngp8sg5KeBBHbeQIL72CF?usp=sharing



Comments